 siggraph
siggraph
siggraph
siggraph
Geometry and Shape
 Full Conference Pass
Full Conference Pass Full Conference 1-Day Pass
Full Conference 1-Day Pass
Date/Time: 28 November 2017, 02:15pm - 04:00pm
Venue: Amber 2
Location: Bangkok Int'l Trade & Exhibition Centre (BITEC)
Session Chair: Hao Li, University of Southern California, USA
Sketch-Based Implicit Blending
Summary: Implicit primitives can be combined by using composition operators, but designing these operators is a complex task. We present an automatic method for deriving an operator simply from 2D sketches. Resulting operators can then be applied in any context (2D/3D) where the same shape or behavior is desired.
Author(s): Baptiste Angles, University of Victoria, IRIT - Université Paul Sabatier
Marco Tarini, CNR-ISTI
Andrea Tagliasacchi, University of Victoria
Loic Barthe, IRIT - Université Paul Sabatier
Brian Wyvill, University of Victoria
Speaker(s): Baptiste Angles, University of Victoria, Université de Toulouse, and IRIT / CNRS

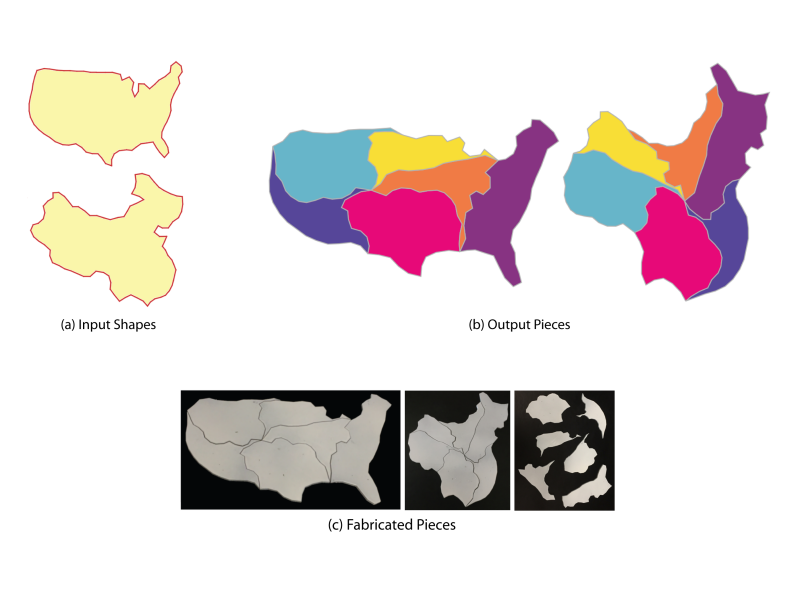
Approximate Dissections
Summary: A geometric dissection is a set of pieces which can be assembled in different ways to form distinct shapes. Existing dissection design techniques are limited to simple, abstract shapes. We introduce a technique which supports complex naturalistic shapes by only requiring that the pieces reconstruct the shapes approximately.
Author(s): Noah Duncan, University of California Los Angeles
Lap-Fai Yu, University of Massachusetts Boston
Sai-Kit Yeung, Singapore University of Technology and Design
Demetri Terzopoulos, University of California Los Angeles
Speaker(s): Noah Duncan, University of California Los Angeles
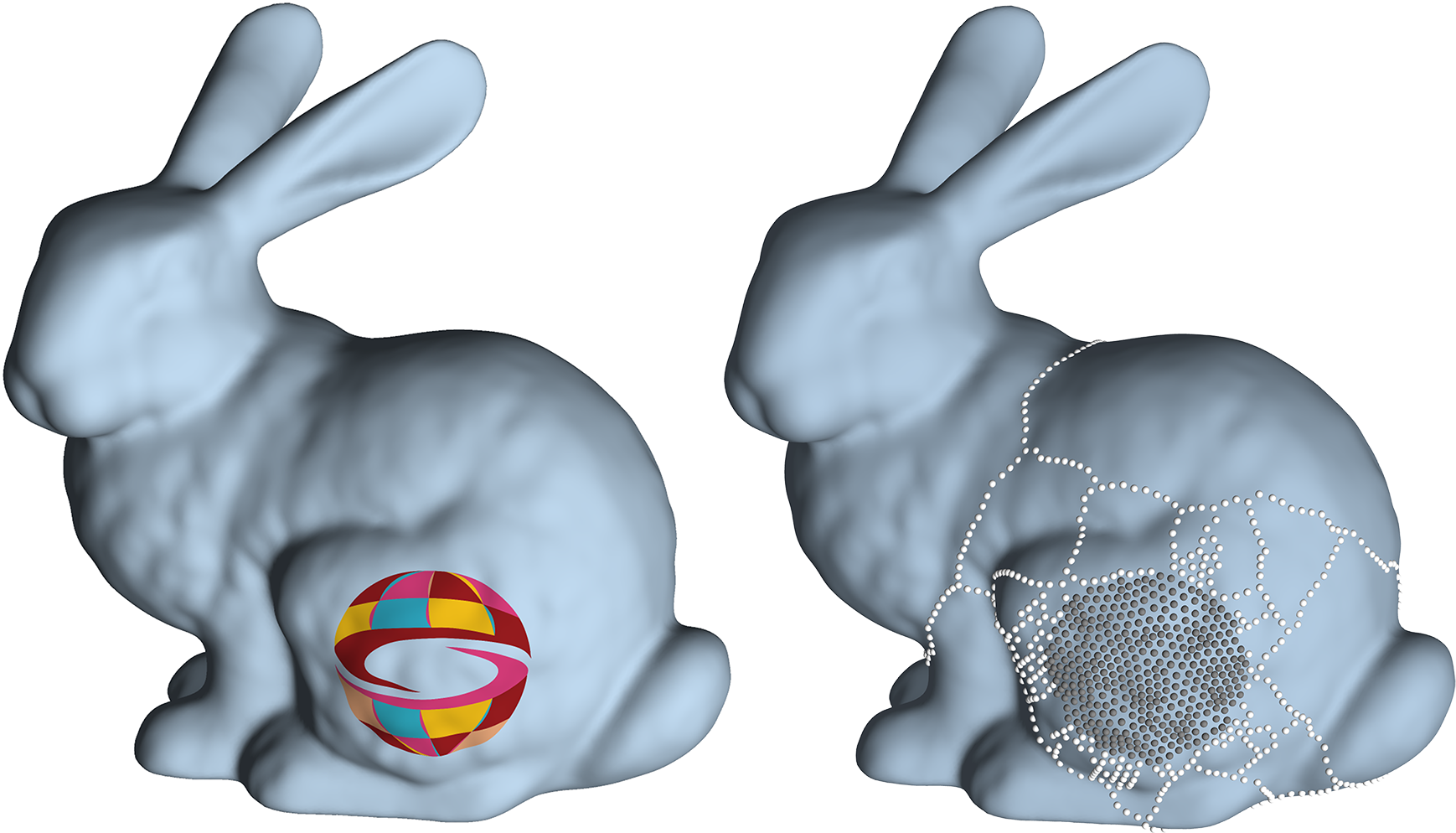
Localized Solutions of Sparse Linear Systems for Geometry Processing
Summary: To solve linear systems in geometry processing Cholesky factorizations are employed in many cases. We demonstrate how to exploit sparsity in both, the right-hand side and the set of desired solution values, to obtain significant speedups during forward and back substitution.
Author(s): Philipp Herholz, TU Berlin
Tim Davis, Computer Science, Texas A&M
Marc Alexa, TU Berlin
Speaker(s): Philipp Herholz, TU Berlin
DS++: A Flexible, Scalable and Provably Tight Relaxation for Matching Problems
Summary: We present a convex relaxation for approximately solving correspondence problems which is provably stronger than the doubly stochastic and spectral relaxations, with the same scalability as the doubly stochastic relaxation. To obtain meaningful integer solutions we suggest a convex-to-concave method which improves upon the standard closest permutation projection.
Author(s): Nadav Dym, Weizmann Institute of Science
Haggai Maron, Weizmann Institute of Science
Yaron Lipman, Weizmann Institute of Science
Speaker(s): Haggai Maron, Weizmann institute of Science


